Special thanks to Vlad Zamfir and Jae Kwon for many of the ideas described in this post
Aside from the primary debate around weak subjectivity, one of the important secondary arguments raised against proof of stake is the issue that proof of stake algorithms are much harder to make light-client friendly. Whereas proof of work algorithms involve the production of block headers which can be quickly verified, allowing a relatively small chain of headers to act as an implicit proof that the network considers a particular history to be valid, proof of stake is harder to fit into such a model. Because the validity of a block in proof of stake relies on stakeholder signatures, the validity depends on the ownership distribution of the currency in the particular block that was signed, and so it seems, at least at first glance, that in order to gain any assurances at all about the validity of a block, the entire block must be verified.
Given the sheer importance of light client protocols, particularly in light of the recent corporate interest in “internet of things” applications (which must often necessarily run on very weak and low-power hardware), light client friendliness is an important feature for a consensus algorithm to have, and so an effective proof of stake system must address it.
Light clients in Proof of Work
In general, the core motivation behind the “light client” concept is as follows. By themselves, blockchain protocols, with the requirement that every node must process every transaction in order to ensure security, are expensive, and once a protocol gets sufficiently popular the blockchain becomes so big that many users become not even able to bear that cost. The Bitcoin blockchain is currently 27 GB in size, and so very few users are willing to continue to run “full nodes” that process every transaction. On smartphones, and especially on embedded hardware, running a full node is outright impossible.
Hence, there needs to be some way in which a user with far less computing power to still get a secure assurance about various details of the blockchain state – what is the balance/state of a particular account, did a particular transaction process, did a particular event happen, etc. Ideally, it should be possible for a light client to do this in logarithmic time – that is, squaring the number of transactions (eg. going from 1000 tx/day to 1000000 tx/day) should only double a light client’s cost. Fortunately, as it turns out, it is quite possible to design a cryptocurrency protocol that can be securely evaluated by light clients at this level of efficiency.
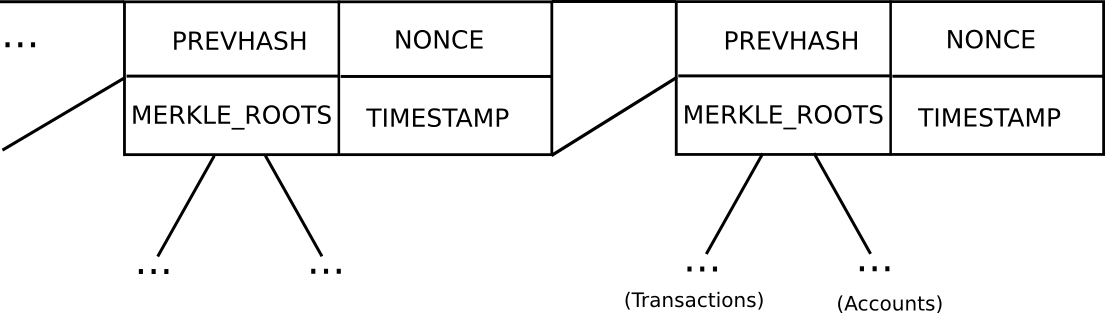
Basic block header model in Ethereum (note that Ethereum has a Merkle tree for transactions and accounts in each block, allowing light clients to easily access more data)
In Bitcoin, light client security works as follows. Instead of constructing a block as a monolithic object containing all of the transactions directly, a Bitcoin block is split up into two parts. First, there is a small piece of data called the block header, containing three key pieces of data:
- The hash of the previous block header
- The Merkle root of the transaction tree (see below)
- The proof of work nonce
Additional data like the timestamp is also included in the block header, but this is not relevant here. Second, there is the transaction tree. Transactions in a Bitcoin block are stored in a data structure called a Merkle tree. The nodes on the bottom level of the tree are the transactions, and then going up from there every node is the hash of the two nodes below it. For example, if the bottom level had sixteen transactions, then the next level would have eight nodes: hash(tx[1] + tx[2]), hash(tx[3] + tx[4]), etc. The level above that would have four nodes (eg. the first node is equal to hash(hash(tx[1] + tx[2]) + hash(tx[3] + tx[4]))), the level above has two nodes, and then the level at the top has one node, the Merkle root of the entire tree.
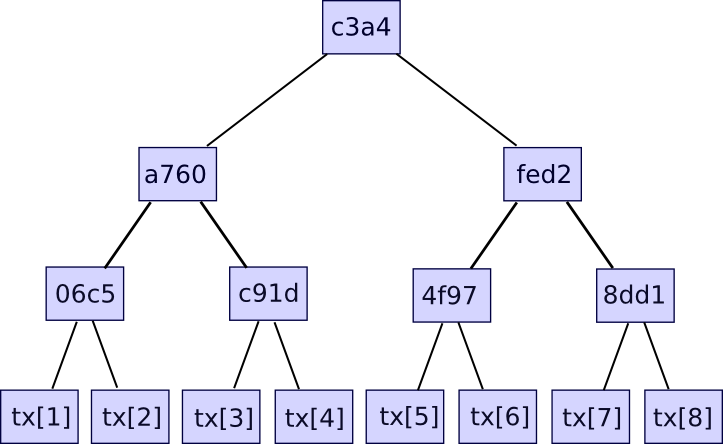
The Merkle root can be thought of as a hash of all the transactions together, and has the same properties that you would expect out of a hash – if you change even one bit in one transaction, the Merkle root will end up completely different, and there is no way to come up with two different sets of transactions that have the same Merkle root. The reason why this more complicated tree construction needs to be used is that it actually allows you to come up with a compact proof that one particular transaction was included in a particular block. How? Essentially, just provide the branch of the tree going down to the transaction:
The verifier will verify only the hashes going down along the branch, and thereby be assured that the given transaction is legitimately a member of the tree that produced a particular Merkle root. If an attacker tries to change any hash anywhere going down the branch, the hashes will no longer match and the proof will be invalid. The size of each proof is equal to the depth of the tree – ie. logarithmic in the number of transactions. If your block contains 220 (ie. ~1 million) transactions, then the Merkle tree will have only 20 levels, and so the verifier will only need to compute 20 hashes in order to verify a proof. If your block contains 230 (ie. ~1 billion) transactions, then the Merkle tree will have 30 levels, and so a light client will be able to verify a transaction with just 30 hashes.
Ethereum extends this basic mechanism with a two additional Merkle trees in each block header, allowing nodes to prove not just that a particular transaction occurred, but also that a particular account has a particular balance and state, that a particular event occurred, and even that a particular account does not exist.
Verifying the Roots
Now, this transaction verification process all assumes one thing: that the Merkle root is trusted. If someone proves to you that a transaction is part of a Merkle tree that has some root, that by itself means nothing; membership in a Merkle tree only proves that a transaction is valid if the Merkle root is itself known to be valid. Hence, the other critical part of a light client protocol is figuring out exactly how to validate the Merkle roots – or, more generally, how to validate the block headers.
First of all, let us determine exactly what we mean by “validating block headers”. Light clients are not capable of fully validating a block by themselves; protocols exist for doing validation collaboratively, but this mechanism is expensive, and so in order to prevent attackers from wasting everyone’s time by throwing around invalid blocks we need a way of first quickly determining whether or not a particular block header is probably valid. By “probably valid” what we mean is this: if an attacker gives us a block that is determined to be probably valid, but is not actually valid, then the attacker needs to pay a high cost for doing so. Even if the attacker succeeds in temporarily fooling a light client or wasting its time, the attacker should still suffer more than the victims of the attack. This is the standard that we will apply to proof of work, and proof of stake, equally.
In proof of work, the process is simple. The core idea behind proof of work is that there exists a mathematical function which a block header must satisfy in order to be valid, and it is computationally very intensive to produce such a valid header. If a light client was offline for some period of time, and then comes back online, then it will look for the longest chain of valid block headers, and assume that that chain is the legitimate blockchain. The cost of spoofing this mechanism, providing a chain of block headers that is probably-valid-but-not-actually-valid, is very high; in fact, it is almost exactly the same as the cost of launching a 51% attack on the network.
In Bitcoin, this proof of work condition is simple: sha256(block_header) (in practice the “target” value changes, but once again we can dispense of this in our simplified analysis). In order to satisfy this condition, miners must repeatedly try different nonce values until they come upon one such that the proof of work condition for the block header is satisfied; on average, this consumes about 269 computational effort per block. The elegant feature of Bitcoin-style proof of work is that every block header can be verified by itself, without relying on any external information at all. This means that the process of validating the block headers can in fact be done in constant time – download 80 bytes and run a hash of it – even better than the logarithmic bound that we have established for ourselves. In proof of stake, unfortunately we do not have such a nice mechanism.
Light Clients in Proof of Stake
If we want to have an effective light client for proof of stake, ideally we would like to achieve the exact same complexity-theoretic properties as proof of work, although necessarily in a different way. Once a block header is trusted, the process for accessing any data from the header is the same, so we know that it will take a logarithmic amount of time in order to do. However, we want the process of validating the block headers themselves to be logarithmic as well.
To start off, let us describe an older version of Slasher, which was not particularly designed to be explicitly light-client friendly:
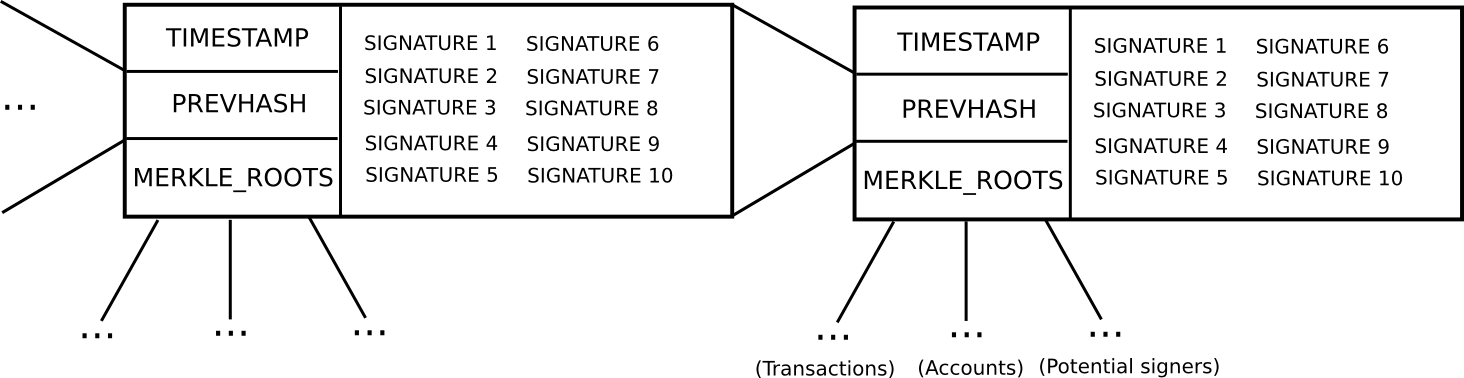
- In order to be a “potential blockmaker” or “potential signer”, a user must put down a security deposit of some size. This security deposit can be put down at any time, and lasts for a long period of time, say 3 months.
- During every time slot T (eg. T = 3069120 to 3069135 seconds after genesis), some function produces a random number R (there are many nuances behind making the random number secure, but they are not relevant here). Then, suppose that the set of potential signers ps (stored in a separate Merkle tree) has size N. We take ps[sha3(R) % N] as the blockmaker, and ps[sha3(R + 1) % N], ps[sha3(R + 2) % N] … ps[sha3(R + 15) % N] as the signers (essentially, using R as entropy to randomly select a signer and 15 blockmakers)
- Blocks consist of a header containing (i) the hash of the previous block, (ii) the list of signatures from the blockmaker and signers, and (iii) the Merkle root of the transactions and state, as well as (iv) auxiliary data like the timestamp.
- A block produced during time slot T is valid if that block is signed by the blockmaker and at least 10 of the 15 signers.
- If a blockmaker or signer legitimately participates in the blockmaking process, they get a small signing reward.
- If a blockmaker or signer signs a block that is not on the main chain, then that signature can be submitted into the main chain as “evidence” that the blockmaker or signer is trying to participate in an attack, and this leads to that blockmaker or signer losing their deposit. The evidence submitter may receive 33% of the deposit as a reward.
Unlike proof of work, where the incentive not to mine on a fork of the main chain is the opportunity cost of not getting the reward on the main chain, in proof of stake the incentive is that if you mine on the wrong chain you will get explicitly punished for it. This is important; because a very large amount of punishment can be meted out per bad signature, a much smaller number of block headers are required to achieve the same security margin.
Now, let us examine what a light client needs to do. Suppose that the light client was last online N blocks ago, and wants to authenticate the state of the current block. What does the light client need to do? If a light client already knows that a block B[k] is valid, and wants to authenticate the next block B[k+1], the steps are roughly as follows:
- Compute the function that produces the random value R during block B[k+1] (computable either constant or logarithmic time depending on implementation)
- Given R, get the public keys/addresses of the selected blockmaker and signer from the blockchain’s state tree (logarithmic time)
- Verify the signatures in the block header against the public keys (constant time)
And that’s it. Now, there is one gotcha. The set of potential signers may end up changing during the block, so it seems as though a light client might need to process the transactions in the block before being able to compute ps[sha3(R + k) % N]. However, we can resolve this by simply saying that it’s the potential signer set from the start of the block, or even a block 100 blocks ago, that we are selecting from.
Now, let us work out the formal security assurances that this protocol gives us. Suppose that a light client processes a set of blocks, B[1] … B[n], such that all blocks starting from B[k + 1] are invalid. Assuming that all blocks up to B[k] are valid, and that the signer set for block B[i] is determined from block B[i – 100], this means that the light client will be able to correctly deduce the signature validity for blocks B[k + 1] … B[k + 100]. Hence, if an attacker comes up with a set of invalid blocks that fool a light client, the light client can still be sure that the attacker will still have to pay ~1100 security deposits for the first 100 invalid blocks. For future blocks, the attacker will be able to get away with signing blocks with fake addresses, but 1100 security deposits is an assurance enough, particularly since the deposits can be variably sized and thus hold many millions of dollars of capital altogether.
Thus, even this older version of Slasher is, by our definition, light-client-friendly; we can get the same kind of security assurance as proof of work in logarithmic time.
A Better Light-Client Protocol
However, we can do significantly better than the naive algorithm above. The key insight that lets us go further is that of splitting the blockchain up into epochs. Here, let us define a more advanced version of Slasher, that we will call “epoch Slasher”. Epoch Slasher is identical to the above Slasher, except for a few other conditions:
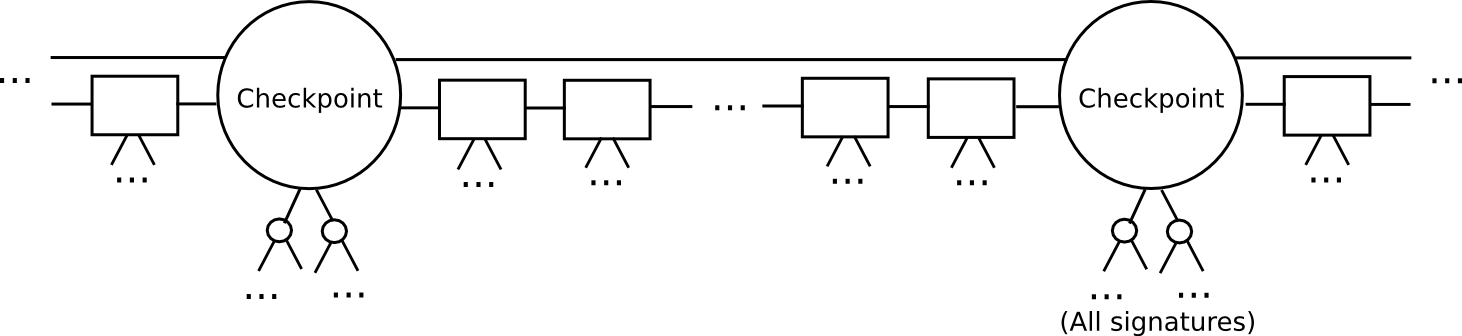
- Define a checkpoint as a block such that block.number % n == 0 (ie. every n blocks there is a checkpoint). Think of n as being somewhere around a few weeks long; it only needs to be substantially less than the security deposit length.
- For a checkpoint to be valid, 2/3 of all potential signers have to approve it. Also, the checkpoint must directly include the hash of the previous checkpoint.
- The set of signers during a non-checkpoint block should be determined from the set of signers during the second-last checkpoint.
This protocol allows a light client to catch up much faster. Instead of processing every block, the light client would skip directly to the next checkpoint, and validate it. The light client can even probabilistically check the signatures, picking out a random 80 signers and requesting signatures for them specifically. If the signatures are invalid, then we can be statistically certain that thousands of security deposits are going to get destroyed.
After a light client has authenticated up to the latest checkpoint, the light client can simply grab the latest block and its 100 parents, and use a simpler per-block protocol to validate them as in the original Slasher; if those blocks end up being invalid or on the wrong chain, then because the light client has already authenticated the latest checkpoint, and by the rules of the protocol it can be sure that the deposits at that checkpoint are active until at least the next checkpoint, once again the light client can be sure that at least 1100 deposits will be destroyed.
With this latter protocol, we can see that not only is proof of stake just as capable of light-client friendliness as proof of work, but moreover it’s actually even more light-client friendly. With proof of work, a light client synchronizing with the blockchain must download and process every block header in the chain, a process that is particularly expensive if the blockchain is fast, as is one of our own design objectives. With proof of stake, we can simply skip directly to the latest block, and validate the last 100 blocks before that to get an assurance that if we are on the wrong chain, at least 1100 security deposits will be destroyed.
Now, there is still a legitimate role for proof of work in proof of stake. In proof of stake, as we have seen, it takes a logarithmic amount of effort to probably-validate each individual block, and so an attacker can still cause light clients a logarithmic amount of annoyance by broadcasting bad blocks. Proof of work alone can be effectively validated in constant time, and without fetching any data from the network. Hence, it may make sense for a proof of stake algorithm to still require a small amount of proof of work on each block, ensuring that an attacker must spend some computational effort in order to even slightly inconvenience light clients. However, the amount of computational effort required to compute these proofs of work will only need to be miniscule.











